벡터끼리의 내적은 매우 유용한 정보를 줄 수 있다.
이를 테면, 인공지능의 다양한 연산에 기초가 되기도 하며,
이미지 인식, 음성 인식 그리고 구매 이력에 기반한 상품 등을 추천할 때 최종 엔진에서 활용되는 연산이기도 하다.
이게 어떻게 가능한 지에 대한 원리를 알아보려면, 우선 내적의 식을 유도할 필요가 있다.
간단하게 내적을 정의해보자
정의) 내적(inner product = dot product)
임의의 두 벡터 \( \mathbf{a}=(a_1, a_2) \) 와 \( \mathbf{b}=(b_1, b_2) \)에 대해서 내적은 다음과 같이 정의될 수 있다.
$$ \mathbf{a} \cdot \mathbf{b} = a_1b_1 + a_2b_2 = \mathbf{b}^T \mathbf{a} $$
이때 내적은 내적의 성질에 의해서 삼각함수를 이용하여 표현할 수 있는데..,


위 삼각형을 우리는 피타고라스 정리를 간단하게 응용하면 \( c^2 \) 의 식으로 표현할 수 있다.
$$ c^2 = (a \text{sin}(\theta))^2 + (b-a \text{cos}(\theta))^2 = a^2 + b^2 - 2ab\text{cos}(\theta) $$
이 식을 벡터를 이용하여 표현하면 아래처럼 표현이 되는데
$$ || a - b ||^2 = ||a||^2 + ||b||^2 -2 ||a|| ||b|| \text{cos}(\theta) $$ ---- (1)
여기서 내적의 정의와 성질에 의해
$$ || \mathbf{a} - \mathbf{b} ||^2 = (\mathbf{a}-\mathbf{b}) \cdot (\mathbf{a}-\mathbf{b}) $$
$$||\mathbf{a}-\mathbf{b}||^2 = ||\mathbf{a}||^2 + ||\mathbf{b}||^2 -2(\mathbf{a} \cdot \mathbf{b})$$
---- (2)
이때 (1)번과 (2)번 식을 비교하면 다음을 얻는다
$$ \textbf{a} \cdot \textbf{b} = || \textbf{a}|| ||\textbf{b}|| \text{cos}(\theta) $$
즉, 아래와 같이 표기할 수 있다.
$$ \text{cos}(\theta) = \frac{\textbf{a} \cdot \textbf{b}}{|| \textbf{a}|| ||\textbf{b}||} $$
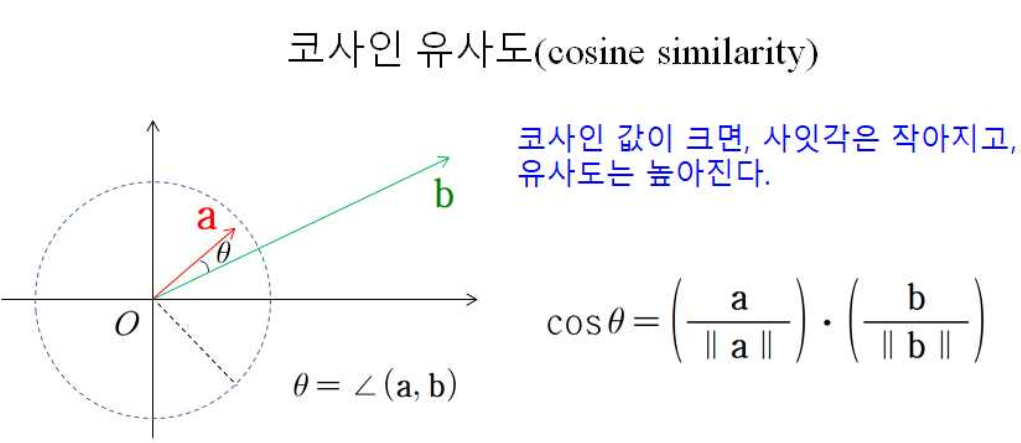
그리고 이는 위의 그림처럼 코사인 유사도로서 나타낼 수 있는 척도가 되는데,
코사인을 좌측으로 두고 식을 재정리해보면, 크기가 항상 1인 단위벡터로 표현이 가능하다는 것을 볼 수 있다. (크기는 무시하겠다는 소리와 같음)
이 성질을 이용하여, 코사인 유사도는 데이터의 크기와 데이터 사이의 거리는 무시하고 단지 데이터의 패턴(방향)만 고려하게 된다.
만약에 코사인 값이 크면, 코사인 함수 성질에 의해 사잇각은 작아지게 되고, 그에 따라 유사도는 높아진다.
반대로 코사인 값이 작으면, 사잇각은 커지게 되고 유사도는 낮아지게 된다.
'선형대수학 > 벡터' 카테고리의 다른 글
| [선형대수] 정사영 (Projection) (1) | 2022.12.23 |
|---|---|
| Norm, 노름, 거리, euclidean distance, 데이터 유사도 (0) | 2022.12.21 |
| 정형데이터 관점에서의 벡터 (0) | 2022.12.21 |
| 일차결합(linear combination) (0) | 2022.12.21 |
